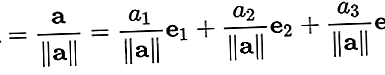수학과 물리학의 벡터는 크기와 방향을 가진 기하학적 객체로 정의 할 수 있습니다. 벡터는 화살표로 표시됩니다. 여기서 화살표의 밑 부분은 벡터의 캐치 포인트 (시작점)를 나타내고, 화살표의 길이는 벡터의 크기 또는 값을 나타냅니다 (화살표가 길수록 값이 커지거나 벡터의 값 및 그 반대)) 화살표는 벡터의 방향을 나타냅니다.

쓰기에서 벡터가 A 지점에서 시작하여 B 지점에서 끝나면 다음과 같은 선 / 화살표가있는 소문자로 쓸 수 있습니다. 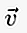 또는
또는 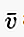 또는 :
또는 :
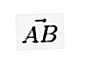
벡터 유형
수학의 벡터는 다음을 포함하여 4 가지 유형으로 나뉩니다.
위치 벡터
시작점이 0 (0,0)이고 끝이 A (a1, a2) 인 벡터입니다.
제로 벡터
"벡터 0"(널 벡터 또는제로 벡터)는 길이가 "0"인 벡터입니다. 이 벡터 좌표의 쓰기는 (0,0,0)이며 일반적으로 기호가 제공됩니다.  , 또는0. 이 벡터는 정규화 할 수 없다는 점에서 다른 벡터와 다릅니다 (즉, 단위 벡터가 0 벡터의 배수가 아님). 벡터의 수는 모든 벡터에서 0입니다.ㅏ 이다ㅏ (그건,0+ㅏ=ㅏ).
, 또는0. 이 벡터는 정규화 할 수 없다는 점에서 다른 벡터와 다릅니다 (즉, 단위 벡터가 0 벡터의 배수가 아님). 벡터의 수는 모든 벡터에서 0입니다.ㅏ 이다ㅏ (그건,0+ㅏ=ㅏ).
제로 벡터에는 명확한 벡터 방향이 없습니다.
단위 벡터
길이가 "1"인 벡터입니다. 일반적으로 단위 벡터는 방향을 나타내는 데만 사용됩니다. 모든 길이의 벡터를 길이로 나누어 단위 벡터를 얻을 수 있습니다. 이것을 벡터 "정규화"라고합니다. 단위 벡터는 다음과 같이 소문자 "a"위에 "캡"으로 표시되는 경우가 많습니다.ㅏ.
벡터를 정규화하려면ㅏ = [ㅏ1, ㅏ2, ㅏ3], 벡터를 길이로 나눕니다 ||ㅏ||. 그래서:
기본 벡터
서로 수직 인 단위 벡터입니다. 2 차원 공간 벡터 (아르 자형2)에는 두 개의 기본 벡터가 있습니다. 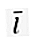 = (1, 0) 및
= (1, 0) 및 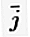 = (0, 1).
= (0, 1).
두 벡터의 유사성
두 벡터의 길이와 방향이 같으면 동일하다고합니다.

두 벡터의 정렬
두 벡터를 나타내는 선이 평행 한 경우 두 벡터를 평행 (병렬)이라고합니다.
벡터 연산
스칼라 곱셈
벡터에 스칼라를 곱하면 벡터도 생성됩니다. 결과 벡터는 다음과 같습니다.
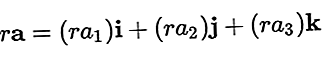
벡터 더하기 및 벡터 빼기
벡터의 예 ㅏ=ㅏ1나는 + ㅏ2제이 + ㅏ3케이 과비=비1나는 + 비2제이 + 비3케이
a 더하기 b의 결과는 다음과 같습니다. 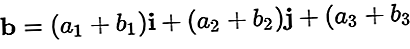
벡터 감소는 + 기호를-기호로 대체하여 적용됩니다.